Pengertian Turunan
Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.
Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan  atau
atau 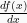 atau y’ dan didefinisikan sebagai:
atau y’ dan didefinisikan sebagai:
Rumus-rumus Turunan Fungsi Aljabar
Dengan definisi turunan akan dicari rumus-rumus turunan fungsi aljabar yang terdiri dari fungsi pangkat  , hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi
, hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi  , dan pangkat dari fungsi
, dan pangkat dari fungsi  .
.
1. Rumus turunan fungsi pangkat 
Fungsi berbentuk pangkat turunannya dapat menggunakan rumus 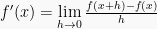 sebagai:
sebagai:
Jadi rumus turunan fungsi pangkat adalah:
2. Rumus turunan hasil kali fungsi 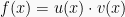
Fungsi f(x) yang terbentuk dari perkalian fungsi u(x) dan v(x), turunannya didapat dengan:
Jadi rumus turunan fungsinya adalah:
3. Rumus turunan fungsi pembagian 
sehingga
Jadi rumus turunan fungsinya adalah
4. Rumus turunan pangkat dari fungsi 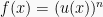
Ingat jika  , maka:
, maka:
Karena 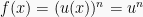 , maka:
, maka:
Atau
Jadi rumus turunan fungsinya adalah:
Rumus-rumus Turunan Trigonometri
Dengan menggunakan definisi turunan, dapat diperoleh rumus-rumus turunan trigonometri berikut: (dengan u dan v masing-masing fungsi dari x)
Aplikasi Turunan
1. Menentukan gradien garis singgung suatu kurva
Gradien garis singgung (m) pada suatu kurva y = f(x) dirumuskan sebagai:
Persamaan garis singgung pada suatu kurva y = f(x) di titik singgung  dirumuskan sebagai:
dirumuskan sebagai:
2. Menentukan interval fungsi naik dan fungsi turun
- Syarat interval fungsi naik
- Syarat interval fungsi turun
3. Menentukan nilai stasioner suatu fungsi dan jenisnya
Jika fungsi y = f(x) kontinu dan diferensiabel di x = a dan f'(x) = 0, maka fungsi memiliki nilai statisioner di x = a. Jenis nilai stasioner dari fungsi y = f(x) dapat berupa nilai balik minimum, nilai balik maksimum, atau nilai belok. Jenis nilai stasioner ini bisa ditentukan dengan menggunakan turunan kedua dari fungsi tersebut.
- Nilai maksimum
dan
Jika  dan
dan 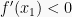 , maka
, maka 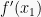 adalah nilai balik maksimum dari fungsi y = f(x) dan titik
adalah nilai balik maksimum dari fungsi y = f(x) dan titik  adalah titik balik maksimum dari kurva y = f(x).
adalah titik balik maksimum dari kurva y = f(x).
- Nilai minimum
dan
Jika  dan
dan  , maka
, maka 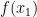 adalah nilai balik minimum dari fungsi
adalah nilai balik minimum dari fungsi  dan titik
dan titik 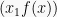 adalah titik balik minimum dari kurva y = f(x).
adalah titik balik minimum dari kurva y = f(x).
- Nilai belok
dan
Jika  dan
dan 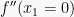 , maka
, maka 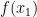 adalah nilai belok dari fungsi y = f(x) dan titik
adalah nilai belok dari fungsi y = f(x) dan titik 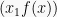 adalah titik belok dari kurva y = f(x).
adalah titik belok dari kurva y = f(x).
4. Menyelesaikan soal limit berbentuk tak tentu  atau
atau 
Jika 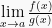 merupakan limit berbentuk tak tentu
merupakan limit berbentuk tak tentu  atau
atau  , maka penyelesaiannya dapat menggunakan turunan, yaitu f(x) dan g(x) masing-masing diturunkan.
, maka penyelesaiannya dapat menggunakan turunan, yaitu f(x) dan g(x) masing-masing diturunkan.
Jika dengan turunan pertama sudah dihasilkan bentuk tertentu, maka bentuk tertentu itu adalah penyelesaiannya. Tetapi jika dengan turunan pertama masih dihasilkan bentuk tak tentu, maka masing-masing f(x) dan f(x) diturunkan lagi sampai diperoleh hasil berbentuk tertentu. Cara penyelesaian seperti ini disebut Dalil L’hopital.
5. Menentukan rumus kecepatan dan percepatan
Jika rumus atau persamaan posisi gerak suatu benda sebagai fungsi waktu diketahui yaitu s = f(t), maka rumus kecepatan dan kecepatannya dapat ditentukan yaitu:
- Rumus kecepatan
- Rumus percepatan
Contoh Soal Turunan Fungsi dan Pembahasan
Contoh Soal 1 – Turunan Fungsi Aljabar
Turunan pertama dari 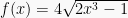 adalah
adalah
Pembahasan 1:
Soal ini merupakan fungsi yang berbentuk y = 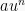 yang dapat diselesaikan dengan menggunakan rumus
yang dapat diselesaikan dengan menggunakan rumus 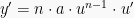 . Maka:
. Maka:
Sehingga turunannya:
Contoh Soal 2 – Turunan Fungsi Trigonometri
Tentukan turunan pertama dari
Pembahasan 2:
Untuk menyelesaikan soal ini menggunakan rumus campuran yaitu  dan juga
dan juga 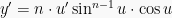 . Sehingga:
. Sehingga:
Contoh Soal 3 – Aplikasi Turunan
Tentukan nilai maksimum dari 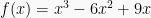 pada interval -1 ≤ x ≤ 3.
pada interval -1 ≤ x ≤ 3.
Pembahasan 3:
Ingat syarat nilai fungsi f(x) maksimum adalah 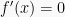 dan
dan  maka:
maka:
jika
dan  dan
dan 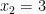



Tidak ada komentar:
Posting Komentar